© The Waters Trust, 2014, All Rights Reserved
Wind Power and the Betz Error
|
In aviation, drag must be minimized to increase performance. The faster an aircraft goes, the more drag is created and the more fuel is used. An aircraft has to penetrate air efficiently. This is why long thin wings are used by sailplanes (lower left picture). They are designed to maximize efficient penetration without an engine.
Drag increases by the square with velocity Aircraft must reduce drag to increase efficiency. In wind power, the goal is to convert wind force into useable energy. The faster the wind blows, the more energy is available. A wind turbine is anchored in a stream of air. Air can be deflected around an obstacle with no penalty. This can significantly increase the amount of energy available despite creating drag.
Force increases by the square with velocity. Wind turbines can use drag to increase efficiency. So
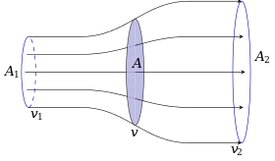
This is because drag is expressed as an instant value where power is expressed over time. A 100w light bulb uses 100w in 1 hour. So if drag increases by the square, the power required increases by the cube, as does the power available in this case. This is explained here and here. To maximize available wind force efficiency, kinetic energy must logically be extracted from as many air molecules passing through a given area as possible. The maximum efficiency of this transfer of energy is expressed as the Betz Limit. The Betz Limit The Betz law applies to all Newtonian fluids. It defines the maximum theoretical efficiency that a wind turbine can achieve as 59.3%. This is based on the total available energy of the wind at a given speed. All current commercial wind turbines are designed based on this same assumption and most wind turbines are considered to be 34% to 45% efficient. This is a huge mistake The Betz limit is based on the obvious assumption that extracting energy from wind will reduce the speed of the wind. Betz only applies to the point of extraction. What the Betz limit ignores, or more correctly, what resultant design assumptions throughout the global wind industry have ignored, is that you can also increase the speed of the wind prior to extracting energy with no penalty. Double the wind speed and the available energy increases by 8 times. The ironic fact is that wind turbine locations often benefit from this principle but not wind turbine designs. Wind farms are often situated along a ridge facing a prevailing wind because a ridge increases wind speed. A mountain ridge is a good example of converting drag to energy. Wind is forced to go over the ridge, thereby compressing and accelerating the air. If the ridge is considered to be part of the design, by placing a wind turbine near the top of a ridge, it becomes obvious that a fixed obstacle (drag) can efficiently increase the amount of energy available. So how does this affect the Betz limit? The Betz limit is correct but only applies to part of the design that extracts energy. It does not apply to what happens before or after that event. The industry wide mistake has occurred by setting the Betz limit as the theoretical maximum efficiency of the complete wind turbine design. This has cost billions of dollars and led to inefficient designs. Betz limited wind turbine designs Currently, only the outer 30% of a typical wind turbine blade produces any meaningful torque and that blade area is less than 5% of the total disk area. In addition, tip loss occurs at the maximum point of leverage. Aerodynamic efficiency is utilized but no attempt is made to divert or accelerate the air prior to or after extraction. In other words, the drag side of the equation is completely ignored. When considered from this perspective, the difference between aircraft and wind turbines becomes obvious. The idea of using a few long thin blades to maximize aerodynamic efficiency is ridiculous. Why try to efficiently penetrate the air when you are anchored to the ground? The primary goal of a wind turbine is to convert the kinetic energy of air molecules into electrical energy. An “efficient” wind turbine produces energy by first maximizing and then extracting energy differential between the air and the ground. As an example, velocity can be first increased using drag, Energy is then extracted within Betz limitations. Drag can then be applied again to increase differential still further. |
|
Wind Turbine Efficiency
So what is an efficient design? In simplest terms, the goal is to accelerate every available molecule and direct it to the region of greatest leverage at maximum velocity like the outside ring of a rotating turbine in my crude example to the left. Notice that there are no blades in the disk and all of the blades are at the maximum point of leverage. The "blades" in this example are deliberately inefficient, made from house foundation vents with no airfoil. This was done to prove that a large percentage of the efficiency gain was not related to airfoil efficiency. Even though this design is clearly not optimized, torque/rpm is considerably higher, cut in speed far lower and wind direction can vary significantly with little efficiency loss. This design has been 3rd party tested to over 120 times more efficient than current designs. This is clearly far beyond the Betz limit. Remember that available energy (watt hours) increases by the cube with velocity. Small changes in wind velocity therefore have a large impact on available energy. In this example, the flat plate obstacle is the “ridge”, forcing air to divert and accelerate before passing through the energy extraction blades at the perimeter – the area of maximum leverage. The more that the air is accelerated and focused, the more energy is available. Additionally, by creating a low pressure void behind the obstacle/ridge/plate or creating vortexes, use of a cone or spiral etc, differential (available energy) can be increased further. Yet again, the only penalty for doing so is drag, which is compensated for by anchoring to the ground. Extracting energy from rivers and tides This primary knowledge becomes even more effective when applied to extracting energy from river and tidal forces. Air can compress. Water cannot. This means that any constriction in water flow is translated directly into increased velocity. Constrict a wide slow river into a narrow channel and you have “rapids”. Triple the speed and you have nine times the force. Focus all of that force towards a point of maximum leverage and the results are predictable. Density of water is approximately 770 times greater than air. This is where it really gets interesting Velocity differential can create thermal differential. This is discussed further here. Conclusion
Reference Drag The mathematical relationship is a little more complex but the general rule is that drag force increases approximately by the square with velocity. In the wind industry, theoretical energy output is estimated to increase by the cube with velocity. https://en.wikipedia.org/wiki/Betz's_law ele.aut.ac.ir/~wind/en/tour/wres/enrspeed.htm http://en.wikipedia.org/wiki/Drag_equation http://en.wikipedia.org/wiki/Drag_(physics) As wind force increases, the drag force increases by the square (instant), and energy available increases by the cube (time). Output is measured in watts, which equates to an hour. A 100 watt light bulb uses 100 wh per hour. Using real world examples, reviewing numerous wind turbine performance charts, typical output in watt/hrs increases between 4 and 9 times as wind speed doubles. . |